从网络验证到 NDD

作为一个偏门的小众领域，一直会有人问起说网络验证是什么？(Network Verification)。参考去年组会上的简单梳理，加上自己浅薄的理解，我也算是成功给大组里别的老师的同门讲明白了我们在做什么。这里只是简单的介绍这个研究方向，并且不涉及到论文层面的内容。

想要解决什么问题？

通常网络服务提供商 (Internet Service Provider, ISP) 是有自己维护的组网，并且由骨干网串联起来，从而为用户提供网络连接。这也就意味着 ISP 以及 ISP 之间的网络对稳定性的要求会极高。除此之外，厂商也会自己组建大型数据中心等设施，会面临频繁的配置变更及动态扩缩容等的需求。所以，就需要一种方案，可以在配置网络时或配置变更时提前验证其准确性和鲁棒性，来为网络增加一层防护。。

除此之外，从软件定义网络 (Software Defined Network, SDN) 的角度考虑，中央控制器作为选出的 Leader 可以获取到全局的拓扑等信息，是不是也可以在其下发之前做建模验证，来保证下发结果的合理性？

想要验证的问题（举例）：

任意两节点之间的可达性
节点转发表
任意 k 条链路断开之后的情况
……

解决方案

所有的解决方案都是在做取舍，这里也不例外。从前到后，我们所验证的真实性在降低，解决方案的实际开发复杂性某种程度上在提升，但是应用的性能和人力开销也在降低。

物理镜像

部署完全相同配置的镜像网络来做物理测试，直接在镜像网络中发送数据包、抓包分析等

虚拟镜像 emulation

同物理镜像，但是使用虚拟机或容器的形式表示每一台网元设备。在容器之间建立同物理网络相同的连接，并真实的模拟数据包在网络中的转发，完整的根据协议的规划进行。

开销大，速度慢

网络仿真 simulation

只模拟转发行为，通过算法直接计算最终的转发表

例如：真实网络中的协议大多通过扩散的方式传播，既然我们已经拿到了全局的拓扑和每个节点的配置信息，我们就可以找到一种方式尽快的模拟出网络稳定之后的转发表

这里我们以最为被广泛使用的 Batfish 开源网络验证工具为例 (1.2k stars)，它将整个网络验证过程划分为了6步：

解析 parsing：解析不同厂商的配置文件，通常是 .cfg 文件，记录着设备的所有功能定义，如端口启用、ip分配、协议配置等
提取 extraction：将上一步解析到的配置信息转为类对象存储，可以理解为对每个厂商都会定义其对应的配置解析类
转换 conversion：去除厂商特定的配置信息，以全局统一的方式存储配置信息，使其厂商无关
后处理 post-processing：解决配置解析中的问题，确保可以进行仿真计算
计算数据平面 data plane generation：计算 RIB，FIB，第一层到第三层overlay实际拓扑
分析转发 forwarding analysis：计算端口谓词等信息，建模转发行为

网络仿真 simulation 怎么做

笼统来说，网络的仿真验证 simulation 会对每台设备的每个端口计算端口谓词 port predicate，也即为可以从这个端口上转发出去的包头空间 header space。这样的话，对从节点 A 到节点 B 的可达性也就转变成了从节点 A 到节点 B 的路径上，所有端口谓词的交集，表达了最终所有可以从 A 到 B 的包头空间，也即所有可以传递的数据包包头。因为一般情况下，后续所需要的验证会大量重复的利用前面所计算出的中间信息，那么我们也就需要一种方式可以更高效紧凑的表示出这部分信息。

包头空间是什么

对于一个数据包来说，最基础的包头空间可以是 ip 五元组（srcIP, srcPort, dstIP, dstPort, protocol），以 ipv4 为例，我们就需要完整表示出两个 ip 地址的 32bit，两个端口的 16bit，协议的 8bit，共 104bit 的包头信息。比如在 Batfish 中，它的 BDDPacket 共表示了：

FIRST_PACKET_VAR // reserved for auxiliary variables before packet vars
   + IP_LENGTH * 4 // primed/unprimed src/dst
   + PORT_LENGTH * 4 // primed/unprimed src/dst
   + IP_PROTOCOL_LENGTH
   + ICMP_CODE_LENGTH
   + ICMP_TYPE_LENGTH
   + TCP_FLAG_LENGTH * 8
   + DSCP_LENGTH
   + ECN_LENGTH
   + FRAGMENT_OFFSET_LENGTH
   + PACKET_LENGTH_LENGTH;

如果想要表示 ipv6 地址，单单是一个 ip 就需要 128bit 的空间来表示。又或者想要表示链路状态等，又需要向内添加额外的 bit 位用来表示。

所以理论上我们所想要表示的包头空间是一个非常庞大的信息域。

如何高效的表示

最开始的验证工具使用 Trie 前缀树的方式来表示。

Trie

有关 Trie 树的相关信息可以参考 LeetCode 208。对于我们想要表示的 01 串（包头空间）来说，字典树应该是一颗三叉树，分别代表 0，1，any。在每个中间节点上都有一个 isEnd 的标记位，用来表示当前节点可以是 01 串的终点，也即是这一段从根到当前节点的信息完整的表示了一段内容。这里以力扣的原题 java 题解（修改为三叉）为例展示 Trie 的存储和查询结构。

class Trie {
    private Trie[] children;
    private boolean isEnd;

    public Trie() {
        children = new Trie[3];
        isEnd = false;
    }
    
    public void insert(int[] word) {
        Trie node = this;
        for (int i = 0; i < word.length(); i++) {
            int index = word[i];
            if (node.children[index] == null) {
                node.children[index] = new Trie();
            }
            node = node.children[index];
        }
        node.isEnd = true;
    }
    
    public boolean search(int[] word) {
        Trie node = searchPrefix(word);
        return node != null && node.isEnd;
    }
    
    public boolean startsWith(int[] prefix) {
        return searchPrefix(prefix) != null;
    }

    private Trie searchPrefix(int[] prefix) {
        Trie node = this;
        for (int i = 0; i < prefix.length(); i++) {
            int index = prefix[i];
            if (node.children[index] == null) {
                return null;
            }
            node = node.children[index];
        }
        return node;
    }
}

但是，Trie 树对 any 的表示是一条单独的路径，作为树结构也无法复用下层的子树。这会导致整颗树很胖，很冗余，查询和遍历都很复杂，需要一直判断当前节点是否已经标记了 isEnd。尽管 Trie 能表示出离散的空间，但是在网络验证工具的表达中，它将离散的同一等价类（具有相同转发行为的包）需要拆分表示。以 Veriflow 为例，它对 TrieNode 的定义如下：

class TrieNode
{
public:
    TrieNode* parent;
    TrieNode* zeroBranch;
    TrieNode* oneBranch;
    TrieNode* wildcardBranch;
    Trie* nextLevelTrie;
    unordered_set< Rule, KHash< Rule >, KEqual< Rule > >* ruleSet;

    TrieNode();
    ~TrieNode();
};

可以看到，在 Veriflow 里，已经有了对域划分的思想。

在对等价类的表示中，Trie 无法合并多个 range，只能将每个 range 当作一个等价类，从而产生了不必要的拆分。并且可以预想到，在对连续范围的非离散数据表示中，Trie 结构本身并不能很好的编码信息，只能将所有的可能性都进行表示。

veriflow ec

除此之外，Trie 结构本身也不适合作为逻辑计算的载体。在数据包传播过程中，从单个节点的视角来看，它是上游限制与本地信息的结合，并向下游继续传播的过程，中间不可避免需要涉及到对空间的限制计算。假如我们安排两个 Trie 存储的空间做交集或并集，就需要两个指针从根节点开始向下递归遍历，any 与 0 和 any 与 1 都会造成重新的树结构分裂，牵一发而动全身。

SAT/SMT

布尔可满足性理论（Boolean satisfiability problem，SAT）是用来解决给定的真值方程式，询问是否存在一种解释可以满足给定的布尔公式。换句话说，它询问公式的变量是否可以被一致地替换为 TRUE 或 FALSE 的值，使得公式评估为 TRUE。如果这种情况成立，则该公式称为可满足的，否则为不可满足的。例如，公式 a AND NOT b 是可满足的，因为可以找到 a = TRUE 和 b = FALSE 的值，使得 (a AND NOT b) = TRUE。相比之下，a AND NOT a 是不可满足的。

模理论可满足性（Satisfiability modulo theories，SMT）是确定一个数学公式是否可满足的问题。它将布尔可满足性问题（SAT）推广到更复杂的公式，这些公式涉及实数、整数以及各种数据结构，如列表、数组、位向量字符串等。SMT 求解器是旨在为实际输入子集解决 SMT 问题的工具。

通过 SMT 求解器的方式来对包头空间进行信息表示，可能着重于对包头空间的逻辑计算以及最终是否可满足的求解。但是在预想中，SMT 求解器需要将所有的可能解进行遍历尝试，直到确认存在一组可满足的解。并且随着需要表示信息变得复杂，以及在网络严重工具里解空间的扩张，SMT 可能并不是一种非常高效的建模方式。

由于本人对这方面的接触比较少，只能确认在一些网络验证工具中会用 SMT 的方式建模自己需要验证的内容。

BDD

二元决策图（Binary Decision Diagram），可以视为一颗用于编码表示 01 信息的二叉树，我们可以定义它的 Left/Low/Zero 边代表 0，Right/High/One 边代表 1，any 可以用 0 1 两条边指向同一个子树来表示。如此这般，从一颗 BDD 树的根节点开始向下遍历到叶子节点即为一个 01 串。最终我们将所有叶子节点指向 TRUE 和 FALSE 两个全局的终结点，只有最终指向 TRUE 终结点的信息是我们所要编码的所有信息。

我们期望能通过 BDD 的结构对离散的包头空间进行紧凑表达，并且能方便的进行逻辑限制条件的计算。

在最初始的状态下，BDD 树呈现出下图的样子：

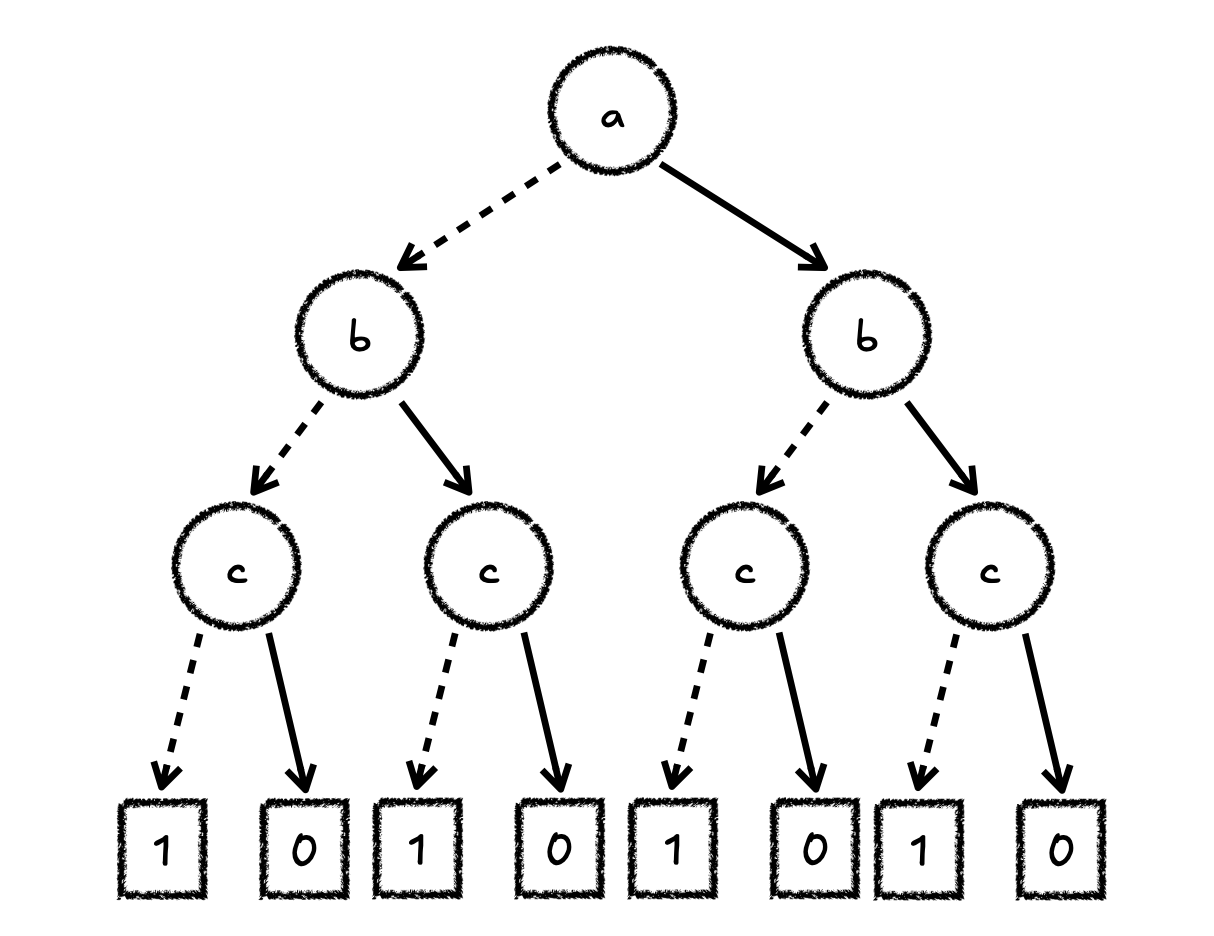
BDD Tree

但是，可以注意到，它是可以被化简的。实际上，BDD 已经是 Reduced Ordered BDD 的简称。在固定变量顺序的表示里，每个编码信息都会被化简后的 BDD 唯一的表示。它的化简约束如下：

(uniqueness) no two distinct nodes $u$ and $v$ have the same variable name and low- and high-successor
(non-redundant tests) no variable node $u$ has identical low- and high-successor

如图表示 BDD 的化简方法

robdd

通过这种方式，我们就可以唯一的表示所有用到的不同的可能性（并复用），并方便的在他们之间进行逻辑计算，即在原树的基础上构建新的树冠。

BDD example

NDD

在最初的表示方法 Trie 树中，已经尝试将划分域的思想应用到底层的表示结构中了。但是这显然在后面直接应用的形式化建模方式里被模糊处理了。其实，我们不止可以把划分域的思想放到网络验证工具里去匹配和约束，也应该在底层表示里将不同域的表示进行划分。由此，我们提出了 Network Decision Diagram，NDD 这种结构，想要更好的对网络验证过程中的包头空间进行建模表示。

fig4

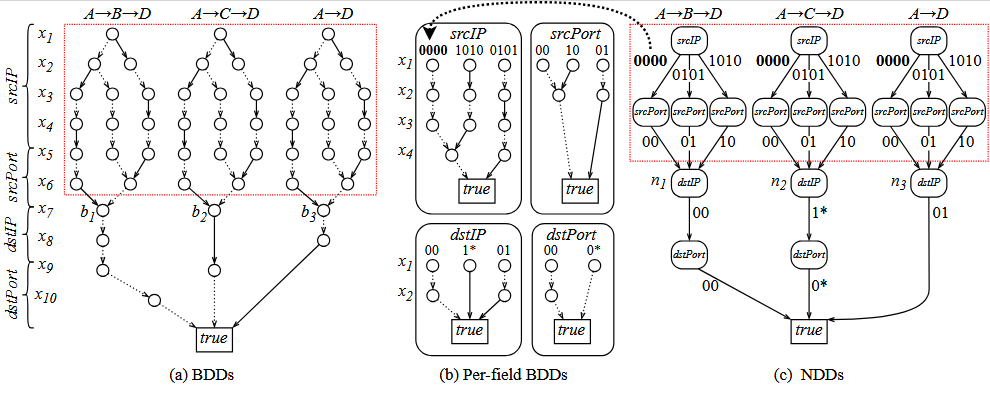
核心点在于，原本 BDD 的表示空间是离散的所有可能性，但是由于在网络验证中所想要表示的信息较多，导致 BDD 结构的肿大。我们通过对每个域之间做解耦，使得 BDD 仅仅需要表示自己域（较少）的信息，从而可以很好的控制住肿大的问题，进而解决了很多 BDD 不够理想的情况。

详细的内容和实现可以移步我们网站进行深入了解。

NDD 的相关工作发表在 NSDI 2025 会议上，并获得了 Outstanding Paper 奖。

Augists-ZDCZ

From Network Verification to NDD