- 历史
- Claude Elwood Shannon 信息论之父 布尔代数的电子实现和应用
- IBM Lucifer Cipher 128 位密钥作分组加密
- Whitfield Diffie and Matin Hellman 首次提出适用网络保密通信的公开密钥思想
- Ronald Rivest, Adi Shamir, Len Adleman 第一次提出公开密钥密码系统的实现方法 RSA
- Abbas El Gamal 提出概率密码系统 ElGamal 方法
- 理论安全与实际安全
- 理论安全(无条件安全)Theoretical Secure (Perfect Secure):攻击者无论截获多少密文,都无法得到足够的信息来唯一决定明文。Shannon 理论证明了,想要达到理论安全,加密密钥的长度需要大于等于明文长度,密钥只用一次
- 实际安全(计算上安全)Practical Secure (Computationally Secure):如果攻击者拥有无限资源,任何密码系统都是可以被破译的;但是,在有限的资源范围内,攻击者都不能通过系统的分析方法来破解系统
- 对称密码与非对称密码
- 对称密码体制(Symmetric System, One-key System, Secret-key System):加密密钥和解密密钥相同,或者一个密钥可以从另一个导出,开放性差
- 非对称密码体制(Asymmetric System, Two-key System, Public-key System):从一个密钥导出另一个密钥是计算上不可行的,开放性好
- 序列密码与分组密码
- 序列密码:密文不仅与最初给定的算法和密钥有关,同时也与明文位置有关(是所处位置的函数)。加密以明文比特为单位,以伪随机序列与明文序列模2加后,作为密文序列
- 分组密码:经过加密所得到的密文仅与给定的密码算法和密钥有关,与被处理的明文数据在整个明文中的位置无关。通常以大于等于64位的数据块为单位,加密得相同长度的密文
- 确定型密码体制与概率密码体制
- 确定型密码:当明文和密钥确定后,密文也就唯一地确定了
- 概率型密码:明文和密钥确定后,密文通过客观随机因素从一个密文集合中产生,密文形式不确定
- 单向函数型密码体制和双向变换型密码体制
- 单向函数型密码体制:适用于不需要解密的场合,容易将明文加密成密文,如哈希函数
- 双向变换型密码体制:可以进行可逆的加密、解密变换
使用对称密码系统的要求
- 强加密算法
- 只有发送方和接收方知道的密钥
对加密信息的攻击类型
- 唯密文攻击:仅知已加密文字(即密文)的情况下进行攻击
- 已知明文攻击:攻击者掌握了某段明文和对应的密文
- 选择明文攻击
- 选择密文攻击
- 选择文本攻击:选择明文攻击和选择密文攻击的结合
- 穷举攻击:可以简单尝试每一个可能的密钥
代换技术
- 将明文字母替换成其他字母、数字或符号的加密方法
- 凯撒密码:每个字母用它之后的第三个字母替换
- 单表代换密码:任意代换,增加密钥空间
- 语言的冗余性导致的密码攻击
- 一次一密
- 与消息一样长且无重复的随机密钥来加密消息,只对一个消息加密,用后丢弃。不可攻破
- 运算基于二进制,按位进行异或运算
- 限制
- 产生大规模的随机密钥有实际困难
- 密钥的分配和保护无法保证
置换技术
- 改变明文内容元素的相对位置,保持内容的表现形式不变
- 通常称为transposition或者permutation密码
- 通过重新安排消息字母的位置来隐藏明文信息,而不是用其他字母来代换明文字母
- 这种方法是很容易破译的,因为密文拥有与明文一样的字母频率统计特性
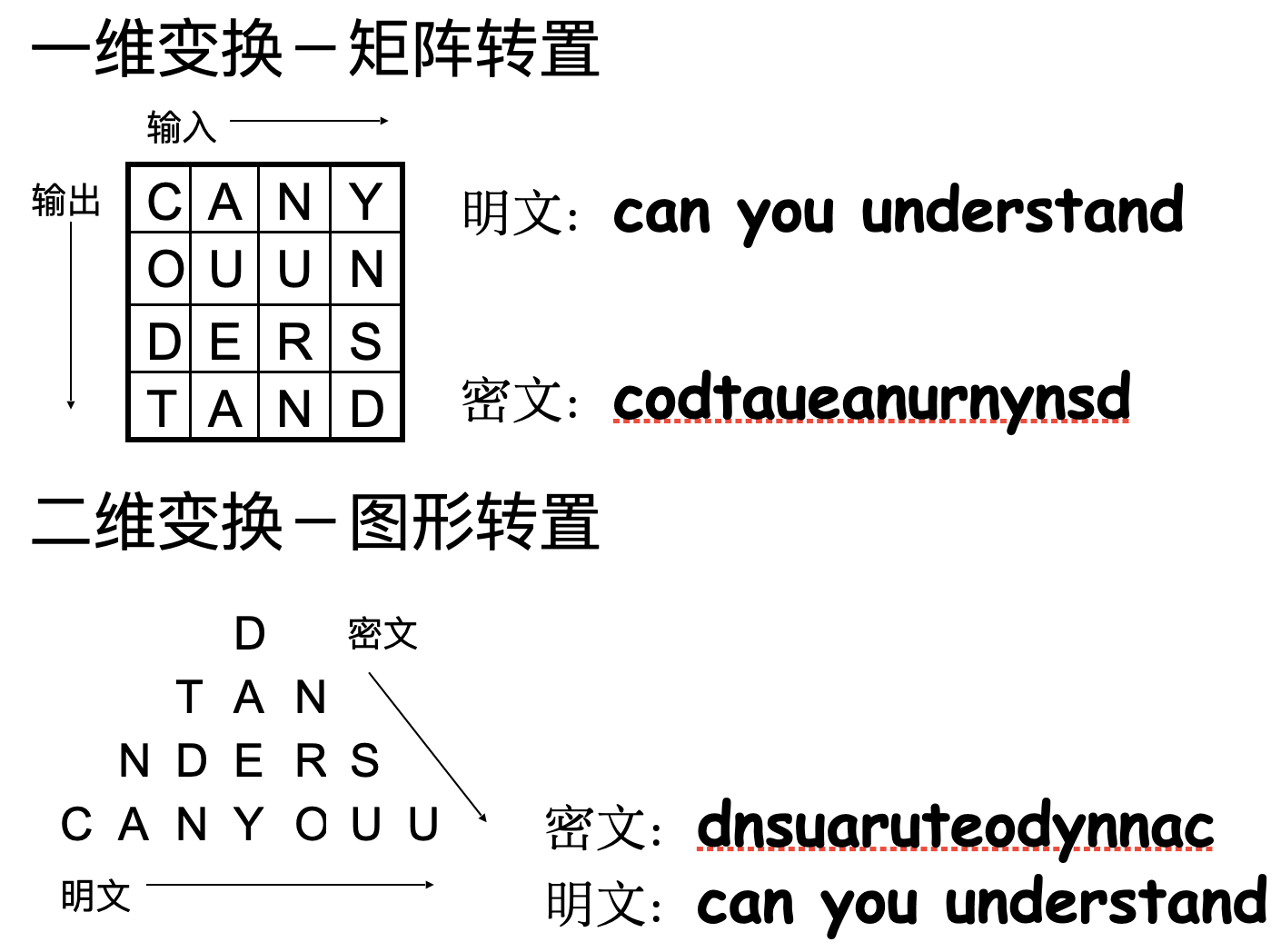
- 栅栏技术 Rail Fence cipher
- 按照对角线的顺序写出明文,按行的顺序读出作为密文

- 按照对角线的顺序写出明文,按行的顺序读出作为密文
隐写术Steganography
- 不是加密技术,只隐藏信息的存在
- 数字水印